|
|
|
| |
|
| |
Fast Adaptive Binary Arithmetic
Coding (M Coder)
Overview: A novel
design of a family of fast table-based adaptive binary arithmetic
coders has been designed. This so-called M coder involves
the innovative features of a table-based interval subdivision in
conjunction with a fast and accurate table-based probability estimator
and a fast bypass coding mode. The computational critical operation of
interval subdivision is approximated by using a pre-quantization of the
range of admissible interval width values induced by renormalization.
Then, for each quantization interval and for each representative
probability value, the corresponding product value is pre-calculated
and stored with suitable precision into a 2-D lookup table. Probability
estimation is performed by employing a finite-state machine with
tabulated transition rules. For approximately uniformly distributed
sub-sources, an optional bypass of the probability
estimator results in an additional speed-up.
A member of the M-coder family has been adopted as a normative part of
the H.264/AVC CABAC entropy coding scheme. This M-coder variant in
H.264/AVC provides virtually the same coding efficiency as a
conventional multiplication- and division-based implementation of
binary arithmetic coding at significantly higher throughput rates
corresponding to speed-up factors in the range of 1.5-2.5. Compared to
the MQ coder (as part of JBIG2 or JPEG2000), an increase in throughput
of up to 18% can be achieved, depending on the implementation platform.
At the same time, the M coder obtains average bit rate savings of
2-4 % relative to the MQ coder in its native H.264/AVC CABAC
environment.
Background: The
discovery of arithmetic codes using a finite-precision arithmetic,
independently achieved by RISSANEN
and PASCO in 1976, can be considered
as the origin of practical arithmetic coding. Since that time many
researchers have contributed to the evolution of arithmetic coding as a
purely academic research topic towards a practical coding method. The
main advantages of arithmetic codes compared to the more popular
variable-length codes (VLCs) can be summarized as follows.
- Entropy
approximation: Arithmetic coding allows to assign
a non-integer number of bits to each symbol to encode and therefore, it
is able to generate a code with a compression performance that comes
arbitrary close to the theoretical lower bound.
- Adaptivity:
The usage of relatively simple adaptation mechanisms enables an
arithmetic coder to adapt to the underlying source statistics.
- Higher-order
modeling: Due to a simple interface between
arithmetic coding and statistical modeling, higher-order statistical
redundancies can be efficiently removed by the usage of appropriately
designed context models.
However, compared to VLCs, the usage of arithmetic codes, in general, involves much
higher computational costs due to the inherently sequentially organized
operation of recursive interval subdivision. Moreover, in an adaptive
coding approach, there is the closely related task of estimating the
symbol probabilities based on previously encoded/decoded symbols, which
generally results in additional nontrivial computational complexity.
Although numerous fast variants of adaptive binary
arithmetic coding were invented and implemented into practical coding
schemes, there is an enduring interest in developing more efficient
variants of arithmetic coding that enable even better or more flexible
compromises between coding efficiency and implementation cost.
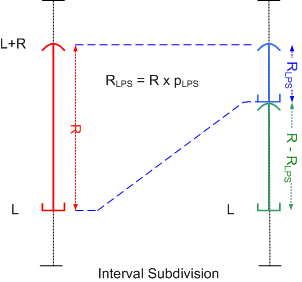Review of the principle of recursive interval subdivision: Suppose that the two possible values '0' and '1' of the binary alphabet are
discriminated according to their estimated probability values, resulting in the
least probable symbol (LPS) and the most probable symbol
(MPS). By keeping track of the value of the MPS (valMPS) and the probability value of
the LPS, denoted as pLPS, a simple
parametrization of the underlying binary alphabet is achieved. Based on that
setting, an initially given interval (as shown in the figure above), which is represented by its lower bound (base) L and
its width (range) R is subdivided into two disjoint subintervals: one interval
of width RLPS = R × pLPS, which is associated with the LPS, and the dual interval of width RMPS = R - RLPS, which is assigned to the MPS. Depending on the
binary value to encode, either identified as the LPS or the MPS, the
corresponding subinterval is then chosen as the new coding interval. By
recursively applying this interval-subdivision scheme to each element
bj of a given sequence of binary decisions b = (b1, b2, …, bN), the
encoder finally determines a value cb in the final subinterval
[L(N), L(N)+ R(N)) that results
after the Nth interval subdivision process.
The (minimal) binary representation of cb is the arithmetic
code of the input sequence b. To ensure that finite-precision registers
are sufficient to represent R(j) and L(j) for all j ∈ {1,2, …, N}, a
renormalization operation is required, whenever R(j) falls
below a certain limit after one or more interval subdivision process(es). By
renormalizing R(j), and accordingly L(j), the leading bits
of the arithmetic code can be output as soon as they are unambiguously
identified.
On the decoder side, the sequence of encoded binary values can be easily
recovered by tracking the interval subdivision step-by-step and by
comparing the bounds of both subintervals to the transmitted binary value of cb representing
the final subinterval. Note that the width R(N) of the final
subinterval is proportional to the product ∏Nj=1 p(bj) of the
individual probabilities of the elements bj of the binary sequence,
such that for signaling the final subinterval, the lower bound of the empirical
entropy of the binary sequence given by -log2 ∏Nj=1 p(bj) = - ∑Nj=1
log2 p(bj) is approximately achieved.
From the standpoint of computational complexity, the most critical
drawback of a straightforward implementation of arithmetic coding is
the multiplication or even division operation required to perform
the interval subdivision in integer arithmetic for each symbol to
encode/decode. Usually, integer multiplications/divisions
are quite expensive operations, especially when realized in
hardware. Therefore, most of the research work in the literature
dealing with the topic of fast binary arithmetic coding is devoted to
the problem of employing a suitable approximation of the multiplication
R × pLPS for determining RLPS. The published work in the
literature can be roughly divided into two categories as follows.
Prior work on fast binary arithmetic coding: The first category of published work on multiplication-free interval subdivision
is based on the idea to approximate either the estimated probabilities
pLPS or the interval width R in such a way
that the multiplication can be replaced by one or more shifts and adds. Therefore, this class of coders are denoted as the
shift-and-add coders. Two typical representatives of this class are the
shift coder of LANGDON and RISSANEN and the CKW scheme of CHEVION et al. While in the former approach pLPS is confined to negative integral powers of 2, the
latter relies on an approximation of the form ½ + r, where r ∈
{2-k | k ∈ |N} for the entire range of admissible values for the interval width
R. In general, however, there is a rather strong
imbalance between the amount of complexity reduction typically achieved by a
shift-and-add coder and the observed degradation in coding efficiency due to the rough approximations involved.
The second and main category of published research
work summarizes all binary arithmetic coding algorithms that are based on the
more radical approach of performing the interval-subdivision process by means of
table-lookup operations only. The most prominent representatives of this
so-called class of table-driven coders are given by the Q
coder (P ENNEBAKER et al.) and its variants QM and
MQ coder, as adopted by JPEG and JPEG2000, respectively. Other techniques belonging to this class are the
quasi-arithmetic coder (H OWARD and VITTER), the Z coder (BOTTOU),
and the ELS coder (WITHERS). As a common
characteristic feature of these table-driven arithmetic coders, a
finite-state machine (FSM) is employed for estimating binary symbol
probabilities.
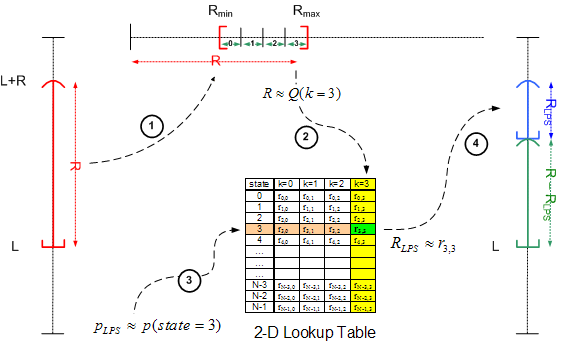Proposed M Coder: The
basic idea of the proposed low-complexity approach of interval
subdivision is to quantize the range of possible interval width values
induced by renormalization into a small number of K cells [JVT-C061].
To further simplify the calculations required to determine quantizer
indices, a uniform quantization with K = 2κ is assumed to be performed, resulting in a set Q =
{Q0,Q1,…,QK-1} of representative interval widths. Together with
the representative set of LPS-related probability values of the FSM given by P =
{p0,p1,…,pN-1}, this quantization enables an approximation of the
exact multiplication R × pLPS by means of a table of K × N
pre-calculated product values {Qk · pn | 0 ≤ k < K; 0 ≤ n < N } in a suitably chosen integer precision. The
entries of the corresponding 2-D lookup table will be
addressed by the (probability) state index n and the quantization cell index
k(R) related to the given value of R, as illustrated above. Computation of the quantizer index k(R) is easily carried out
by a concatenation of a bit-shift and a bit-masking operation, where the latter
can be interpreted as a modulo operation using the operand K = 2κ, hence the naming 'modulo coder' or briefly 'M coder' of the proposed
two-parameter family of coders.
For a fixed choice of the FSM-based estimator, which means that P and N are selected beforehand, the
corresponding family of modulo coders can be parameterized by κ. Usually, only small numbers of κ ∈ {0,1,2,3} are of practical relevance, since the size of
the lookup table is
growing exponentially in κ. Larger values of κ
result in a higher accuracy of the representation of R, but they
require also larger lookup tables. In most practical cases, the choice
of a suitable κ and the selection of an appropriate
probability estimator has to be simultaneously optimized. For H.264/AVC
the optimal choice of the free parameters κ and N was determined under the constraint for the lookup table size of 2κ·N ≤
256 bytes, where each table entry was represented with an 8-bit integer
precision. Obviously, the optimization process depends on the
statistical nature of the given data. For a representative test set of
video sequences encoded under different coding conditions within the
H.264/AVC video coder, a configuration of (κ,
N) = (2,64) was found to be optimal. This configuration is used for the
standardized M coder variant of H.264/AVC. Note that the case κ =
0 is conceptually equivalent to the Q coder approximation. Hence, the M
coder concept can be considered as a generalization of the Q coder and
its derivatives of QM and MQ coder.
Additional speed-up can be obtained by using a bypass of the probability
estimation for approximately uniformly distributed binary symbols. This kind of
sources is often observed in transform coders, where, e.g., signs of transform
coefficients or least significant bits of absolute values of quantized transform
coefficients can be assumed to be uniformly distributed. Therefore, the M coder contains a
simplified interval subdivision in the so-called bypass coding mode based on a hard-wired
equipartition. In this way, the whole bypass encoding/decoding process (including
renormalization) can be realized by nothing more than a shift, a comparison, and
for half of the symbols an additional subtraction.
Performance evaluation of the M Coder: In
a set of coding experiments, the relative performance of the M coder in
comparison to the MQ coder and to a conventional binary arithmetic
coder has been evaluated in the CABAC environment of H.264/AVC. As a
first remarkable outcome of these experiments, it was observed that in
terms of coding efficiency, the specific M coder implementation of
H.264/AVC achieves virtually the same performance in terms of
coding efficiency as an implementation of conventional binary
arithmetic coding based on multiplication and division operations in
16-bit integer arithmetic.
This experimental observation can be interpreted as a verification of the
following analytical study of the approximation effects in the interval
subdivision process. As a measure of inefficiency caused by the subdivision
approximation, the so-called excess codelength or relative
entropy D(p,p') is given as follows:
| D(p,p') |
= - p log2 |
p'
p
|
- (1-p) log2 |
1-p'
1-p
|
, where |
p'=
|
Q(R)
R |
·p |
where p is the actual LPS probability and p' denotes the approximation of the
probability p due to the quantization Q(R) of the LPS related value of interval
width R=RLPS.
However, instead of evaluating the absolute values of excess codelength
D(p,p'), a more meaningful measure is obtained by computing the
inefficiency D(p,p') relative to the entropy H(p) (as the average ideal
codelength):
| δ(p,p') |
= |
D(p,p')
H(p)
|
, where H(p) = -p log2 p - (1-p) log2 (1-p). |
Under the assumption that the probability p is fixed with values in P =
{p0, p1, …, pN-1}, the worst case relative excess codelength
δmax(κ) = max{δ (p,p') | p ∈ P, Q(R) ∈ Q(κ)} can be computed for different choices of κ. It
turns out that for κ = 1, δmax is equal to 0.047,
whereas δmax(k = 2) < 0.013 and δmax(κ) < 0.003 for κ ≥ 3. These values, however,
represent the largest relative increase in codelength that can be expected for
the largest possible quantization error given by sup |R
- Q(R)|.
To calculate the average relative excess codelength δavg(p,p') = E[δ(p,p')], a distribution must be assumed for R.
Empirically, an 1 / R distribution has been determined for typical sequences of
symbols to encode, and based on this empirical distribution the average relative
excess codelength δavg has
been computed for each fixed probability state. As shown in the graph above, δ avg is less than 0.83% for κ = 1 and
less than 0.2% of the ideal codelength for κ
= 2 (i.e., the H.264/AVC related M coder realization, shown as the
magenta colored curve). This numerical estimation proves that the loss
in coding efficiency due to the table-based interval subdivision is
practically negligible, at least in case of a static probability
distribution and for the choice of κ ≥
2. By the same kind of analysis it can be shown that the average
relative excess codelength resulting from a discretization of the
probability space is also negligible (less than 0.05% of the ideal
codelength for N = 64).
Related publications:
D.
Marpe, H. Schwarz, and T. Wiegand: Context-Based
Adaptive Binary Arithmetic Coding in the H.264 / AVC Video Compression
Standard, IEEE Transactions on Circuits and Systems
for Video Technology, Vol. 13, No. 7, pp. 620-636, July 2003,
invited paper. [PDF]
Errata: On p. 631, left column below
Table VI, "max(...)" must be replaced by
"min(...)" in the two
expressions for specifying context index increments for bins related to
absolute values of transform coefficients.
D.
Marpe and T. Wiegand: A Highly Efficient
Multiplication-Free Binary Arithmetic Coder and Its Application in
Video Coding, Proc. IEEE International Conference
on Image Processing (ICIP 2003), Barcelona, Spain, Sept.
2003. [PDF]
D. Marpe, G.
Marten, H. L. Cycon: A
Fast Renormalization Technique for H.264/MPEG4-AVC
Arithmetic Coding,
Proc.
51st Internationales
Wissenschaftliches Kolloquium
(IWK), Ilmenau University of Technology, Ilmenau, Germany, September
11-15, 2006. [PDF]
Related standard contributions (in chronological
order, as
listed here):
[JVT-C061], [JVT-F040], [JVT-U084]
Back
to Home Page Detlev Marpe
|
|
|
Start
Staff